Sprawdzanie II zasady dynamiki dla ruchu obrotowego
Marcin Ratajczyk, Jakub Żogała - klasa 3d, rok szkolny 2008/2009
NOTATKA TEORETYCZNA:
MOMENT BEZWŁADNOŚCI
Moment bezwładności bryły jest równy sumie iloczynów mas poszczególnych elementów bryły i kwadratów ich odległości od osi obrotu.
TWIERDZENIE STEINERA
Moment bezwładności bryły  względem dowolnej osi
względem dowolnej osi  jest równy sumie momentu bezwładności
jest równy sumie momentu bezwładności  względem osi
względem osi  przechodzącej przez środek masy i równoległej do osi
przechodzącej przez środek masy i równoległej do osi  oraz iloczynu masy bryły i kwadratu odległości
oraz iloczynu masy bryły i kwadratu odległości  między osiami.
między osiami.
I ZASADA DYNAMIKI DLA RUCHU OBROTOWEGO BRYŁY
Jeśli suma momentów sił działających na bryłę sztywną, czyli wypadkowy moment siły względem osi obrotu jest równy zeru, to bryła pozostaje w spoczynku lub porusza się ruchem obrotowym ze stałą prędkością kątową wokół tej osi.
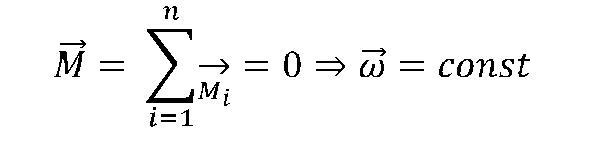
II
ZASADA DYNAMIKI DLA RUCHU OBROTOWEGO BRYŁY
Jeśli wypadkowy moment sił działających na bryłę jest różny od zera, to bryła porusza się zmiennym ruchem obrotowym z przyśpieszeniem kątowym wprost proporcjonalnym do wypadkowego momentu sił, a odwrotnie proporcjnalnym do momentu bezwładności bryły względem wybranej osi obrotu.
III
ZASADA DYNAMIKI DLA RUCHU OBROTOWEGO BRYŁY
Jesli ciało A działa na ciało B momentem siły MAB, to równoczesnie ciało B działa na A
momentem siły MBA, przy czym MAB= - MBA.
DOŚWIADCZENIE:
OPIS URZĄDZENIA
Urządzenie składa się z wahadła Oberbecka oraz z ruchomego bloczka przez który jest przerzucona nić. Wahadło Oberbecka składa się z walca obracającego się na łożyskach w odpowiednim uchwycie oraz czterech symetrycznych ramion w kształcie prętów, wzdłuż których mogą przesuwać się ciężarki. Wahadło rozpędzane jest przy pomocy obciążników zawieszonych na nici nawiniętej na walec osadzony na osi. Moment bezwładności wahadła zmieniamy przez przemieszczanie ciężarków względem osi lub wykręcanie prętów z ciężarkami.

ROZKŁAD SIŁ

SPRAWDZANIE DRUGIEJ ZASADY DYNAMIKI DLA RUCHU OBROTOWEGO
Sprawdzenie drugiej zasady, przy ustalonym  - moment bezwładności badanego ciała w naszym przypadku wahadła Oberbecka, sprowadza się do znalezienia zależności:
- moment bezwładności badanego ciała w naszym przypadku wahadła Oberbecka, sprowadza się do znalezienia zależności:

gdzie:  - to przyśpieszenie kątowe wahadła.
- to przyśpieszenie kątowe wahadła.
Moment siły obliczamy z zależności:
 gdzie:
gdzie:  jest masą obciążnika zawieszanego na nitce nawiniętej na walec o
promieniu
jest masą obciążnika zawieszanego na nitce nawiniętej na walec o
promieniu  współosiowy z osią wahadła,
współosiowy z osią wahadła, 

Obliczamy całkowity moment bezwładności wahadła.
Moment bezwładności pręta względem osi prostopadłej przechodzącej przez środek pręta wynosi:
Korzystamy z twierdzenia Steinera, dla obliczenia momentu bezwładności pręta względem osi prostopadłej przechodzącej przez koniec pręta.

Odważniki na prętach traktujemy jak punkty materialne o momencie bezwładności równym:
Całkowity moment bezwładności wynosi:
Legenda:
R- promień walca, współosiowy z osią wahadła,
na który jest nawinięta nić.
m- masa odważników zawieszona na nitce.
M- moment sił działający na wahadło.
h- wysokość z jakiej spadają odważniki.
t- czas w jakim odważnik pokonuje wysokość h.
a- przyspieszenie liniowe odważników.
ε- przyśpieszenie kątowe wahadła.
Zestawienie wyników doświadczenia:
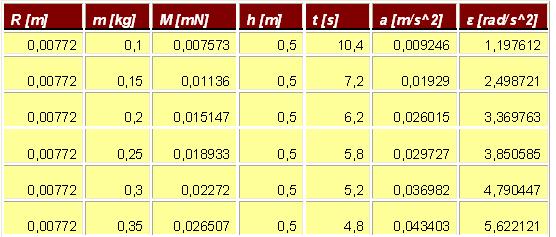

Wniosek:
Przyśpieszenie kątowe jest wprost proporcjonalne do działającego wypadkowego momentu siły 
Zestawienie wyników doświadczenia
Wniosek:
Wykres zależności przyśpieszenia kątowego od momentu bezwładności wahadła jest hiperbolą, więc moment bezwładności jest odwrotnie proporcjonalny do przyśpieszenia kątowego ciała. 
Strona w edycji

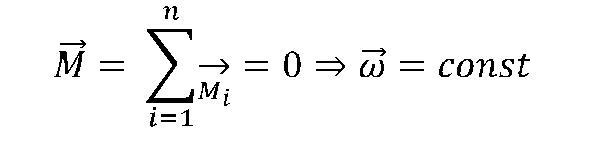


![]() - moment bezwładności badanego ciała w naszym przypadku wahadła Oberbecka, sprowadza się do znalezienia zależności:
- moment bezwładności badanego ciała w naszym przypadku wahadła Oberbecka, sprowadza się do znalezienia zależności:
![]() - to przyśpieszenie kątowe wahadła.
- to przyśpieszenie kątowe wahadła.